दोस्तों कैसे हो मेरा नाम है शिवा सिंह आज मैं आपको बेलनाकार संधारित्र का व्यंजक कैसे निकाला जाए उसके बारे में पूरी जानकारी दूंगा।
बेलनाकार संधारित्र का व्यंजक
चित्रानुसार बेलनाकार संधारित्र प्रदर्शित है। जिसमें धातु के दो बेलन A और B है। जिनके बीच परावैद्युत माध्यम भरा हुआ है। बेलन B का संबंध पृथ्वी से किया गया है।
जब बेलन A को +Q आवेश दिया जाता है तो प्रेरण द्वारा बेलन B के समीपवर्ती तल पर -Q आवेश दूरवर्ती तल पर +Q आवेश उत्पन्न हो जाता है। +Q आवेश का संबंध प्रथ्वी से कर देते है।
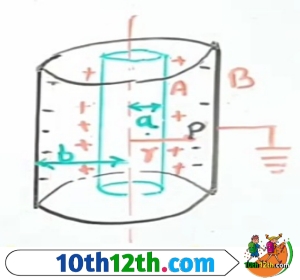
माना बेलन A और बेलन B की त्रिज्याए a और b है। माना कि दोनों बेलनो के मध्य बिंदु P स्थित है जिसकी अक्ष से दूरी r है। तो बिंदु P पर विद्युत क्षेत्र की तीव्रता E = λ/2πε₀rk
एकांक आवेश को विद्युत क्षेत्र के विरुद्ध अल्प दूरी dr विस्थापित करने पर किया गया कार्य
dw = E x (-dr), dw = λ/2πε₀rk (-dr)
इसी प्रकार एकांक आवेश को b से a तक लाने में किया गया कार्य
w = ∫ᵃb.dw, ∫ᵃb λ/2πε₀rk (-dr),
w = -λ/2πε₀k ∫ᵃb 1/r. dr,
w = - λ/2πε₀k [log r]ᵃb,
w = -λ/2πε₀k [log a-log b],
w = λ/2πε₀k [log b- log a],
w = λ/2πε₀k [log b/a]
यही किया गया कार्य विभव के बराबर होगा तब V = A/2πε₀k. log (b/a) चूंकि धारिता C = Q/V, C = Q/λ/2πε₀k. log (b/a) प्रति एकांक लंबाई के लिए धारिता
C = λ/λ/2πε₀k. log (b/a) [चूंकि Q = λ],
C = 2πε₀k. log (a/b) फैरड
वायु या निर्वात में K = 1, C = 2πε₀ log (a/b) फैरड
संधारित्र के प्रकार- समांतर प्लेट संधारित्र, गोलाकार संधारित्र, बेलनाकार संधारित्र।
धारिता बढ़ाने के लिए
- दोनों बेलनों की लंबाई अधिक होनी चाहिए।
- b/a का मान कम से कम होना चाहिए, अर्थात दोनों बेलन लगभग बराबर त्रिज्या के होने चाहिए।
- दोनों बेलनों के बीच ऐसा कुचालक माध्यम भरा होना चाहिए जिसका परावैद्युतांक अधिक हो।

