हेलो, दोस्तों आज की इस पोस्ट के माध्यम से, मैं आपको संख्या पद्धति के बारे में जानकारी देने वाला हूँ, यदि आप जानकारी पाना चाहते हो तो पोस्ट को पूरा पढ़कर जानकारी प्राप्त कर सकते हो।
परिभाषाएं
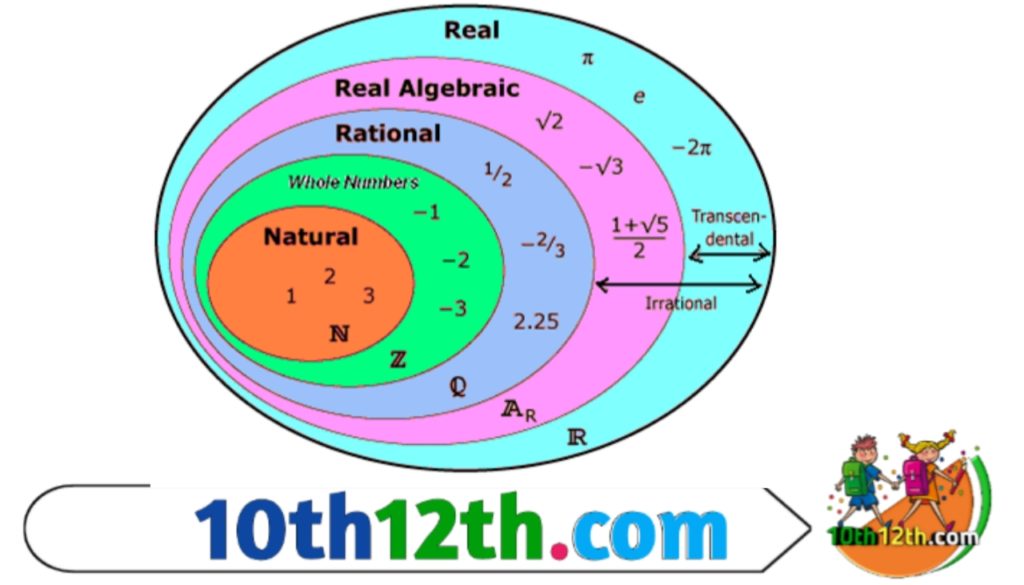
प्राकृत संख्याएँ (Natural Numbers): वस्तुओं को गिनने के लिए जिन संख्याओं का प्रयोग किया जाता है, उन्हें गणन संख्याएँ या ‘प्राकृत संख्याएँ’ कहते हैं।
जैसे- 1, 2, 3, 4, 5,6,7, . . . .
✶ पूर्ण संख्याएँ (Whole Numbers): प्राकृत संख्याओं में शून्य को मिलाने पर जो संख्याएँ प्राप्त होती हैं उन्हें ‘पूर्ण संख्याएँ’ कहते हैं।
जैसे- 0, 1, 2, 3, 4, 5, 6, 7, . . . .
✶ पूर्णांक संख्याएँ (Integers):प्राकृत संख्याओं में शून्य एवं ऋणात्मक संख्याओं को मिलाने पर जो संख्याएँ प्राप्त होती हैं, उन्हें ‘पूर्णांक संख्याएँ’ कहते हैं।
जैसे- -3, -2, -1, 0, 1, 2, 3, . . . .
✶ सम संख्याएँ (Even Numbers): वे संख्याएँ जो 2 से पूर्णतः विभाजित होती हैं उन्हें ‘सम संख्याएँ’ कहते हैं।
जैसे - 2, 4, 6, 8, . . .
✶ विषम संख्याएँ (Odd Numbers) : वे संख्याएँ जो 2 से पूर्णतः विभाजित नहीं होती हैं उन्हें ‘विषम संख्याएँ ’ कहते हैं।
जैसे- 1, 3, 5, 11, 17, 29, 39 , . . . .
✶ अभाज्य संख्याएँ (Prime Numbers): वे संख्याएँ जो स्वयं और 1 के अलावा अन्य किसी संख्या से विभक्त नहीं होती हैं उन्हें ‘अभाज्य संख्याएँ’ कहते हैं।
जैसे- 2, 3, 7, 11, 13, 17 ……….
नोट -‘1’ न तो अभाज्य संख्या है और न ही भाज्य संख्या
✶ भाज्य संख्याएँ (Composite Numbers): वे संख्याएँ जो स्वयं और 1 के अलावा अन्य किसी संख्या से पूर्णतः विभक्त हो जाती हैं ,उन्हें ‘भाज्य संख्याएँ ’ कहते हैं।
जैसे- 4, 6, 8, 9, 10, …………
✶ असहभाज्य संख्याएँ (Co-Prime Numbers) : जब दो या दो से अधिक संख्याओं में कोई भी उभयनिष्ठ गुणनखंड न हो अथवा जिसका म.स. 1 हो ,वे एक साथ ‘सह-अभाज्य संख्याएँ’ कहलाती हैं।
जैसे- (4,9) , (12,25) ,(8,9,12) ।
✶ युग्म-अभाज्य संख्याएँ : ऐसी अभाज्य संख्याएँ जिनके बीच का अंतर 2 हो ‘युग्म-अभाज्य संख्याएँ’ कहलाती हैं।
जैसे- 11, 13✶ परिमेय संख्याएँ (Rational Numbers): वे संख्याएँ जिन्हें pq के रूप में लिखा जा सकता है ,जहाँ p तथा q पूर्णांक हैं एवं q ≠ 0 ‘परिमेय संख्याएँ’ कहलाती हैं ।
जैसे-34,56, 4, 1.77 , 0 , 2.3 ……… ।
✶ अपरिमेय संख्याएँ (Irrational Numbers): वे संख्याएँ जिन्हें pq के रूप में नहीं लिखा जा सकता ,जहाँ p तथा q पूर्णांक हैं एवं q ≠ 0 अपरिमेय संख्याएँ’ कहलाती हैं ।
जैसे - √2, √15 , √2 , 5 1/3 , π आदि✶ वास्तविक संख्याएँ (Real Numbers) :सभी परिमेय तथा अपरिमेय संख्याएँ ‘वास्तविक संख्याएँ’ कहलाती हैं।
जैसे - 4 , 6, 2 ,√7, +4 , -2 आदि ।
✶ काल्पनिक संख्याएँ (Imaginary Numbers) : ऋणात्मक संख्यायों का वर्गमूल लेने पर जो संख्याएं बनती हैं , उन्हें काल्पनिक संख्याएं कहते हैं ।
जैसे -√ - 2, √ - 5
2-महत्वपूर्ण प्रश्न उत्तर-
Q.1. यदि दो अंकों की संख्या के अंको का योग 12 हो तथा अंकों को उलटकर बनायी गयी संख्या मूल संख्या से 18 अधिक हो तो संख्या ज्ञात कीजिए ।
(a) 67 (b) 57 (c) 77 (d) 47
हल :- option से हल करने पर
option (b) 57 से
57 के अंक उलटने पर 75 प्राप्त होगा
75 – 57 = 18
option (b) 57 ने प्रश्न की सभी शर्तों को संतुष्ट किया । यही उत्तर है ।
answer – option (b) 57
number system trick
Q.2. दो अंकों की एक संख्या में , इकाई के स्थान पर अंक दहाई के स्थान पर अंक के दुगूना से 1 कम है । यदि इकाई और दहाई के स्थान पर अंकों को आपस में बदल दिया जाए, तो नई और मूल संख्या के बीच अन्तर मूल संख्या से 20 कम है । मूल संख्या ज्ञात कीजिए ।
(a) 47 (b) 59 (c) 23 (d) 35
हल :- option से हल करने पर
option (a) 47 से
47 अंक उलटने पर 74 होगा
74 – 47 = 27
47 – 27 = 20
Q.3. यदि तीन अंकों वाली किसी संख्या में इकाई और दहाई के अंकों को आपस में बदल दिया जाए तो जो नई संख्या आएगी, वह मूल संख्या से 63 अधिक होगी । इस प्रकार यदि मूल संख्या में इकाई का अंक x हो, तो x के तीनों सम्भव मान क्या होंगे ?
(a) 7, 8, 9, (b) 2, 7, 9 (c) 0, 1, 2 (d) 1, 2, 8
हल :- option से हल करने पर
यहाँ आपको सिर्फ इकाई व दहाई अंक से मतलब है
option (a) 7, 8, 9 से
07 के अंक उलटने पर 70 प्राप्त होगा
70 – 63
18 के अंक उलटने पर 81 प्राप्त होगा
81 – 18 = 63
29 के अंक उलटने पर 92 प्राप्त होगा
92 – 29 = 63
यहाँ option (a) 7, 8, 9, प्रश्न की सभी शर्तों को संतुष्ट करता है । यही उत्तर है ।
Q.4. दो अंकों की किसी संख्या और उन अंकों को आपस में बदल कर बनाई गई संख्या के बीच अन्तर सदा विभाज्य होता है –
(a) 10 से (b) 9 से (c) 11 से (d) 6 से
हल :- 10 के अंक उलटने पर 01 प्राप्त होगा
10 – 01 = 9
12 के अंक उलटने पर 21 प्राप्त होगा
21 – 12 = 9
13 के अंक उलटने पर 31 प्राप्त होगा
31 – 13 = 18
14 के अंक उलटने पर 41 प्राप्त होगा
41 – 14 = 27
अत: इस प्रकार सिद्ध होता है कि उपरोक्त प्रश्न से प्राप्त अन्तर सदैव 9 से विभाज्य है।

