गौस की प्रमेय क्या है?

हेलो, दोस्तों आज की इस पोस्ट के माध्यम से, मैं आपको गौस की प्रमेय के बारे में जानकारी देने वाला हूँ, यदि आप जानकारी पाना चाहते हो तो पोस्ट को पूरा पढ़कर जानकारी प्राप्त कर सकते हो।

गौस की प्रमेय के बारे में

गौस की प्रमेय (Gauss theorem) के अनुसार वायु या निर्वात में किसी विद्युत क्षेत्र में स्थित किसी भी आकार के बंद पृष्ठ से होकर अभिलंबवत गुजरने वाली विद्युत क्षेत्र रेखाओं की संपूर्ण संख्या अर्थात विद्युत फ्लक्स, पृष्ठ के अंदर उपस्थित कुल आवेश की 1/ε₀ गुना होती है।

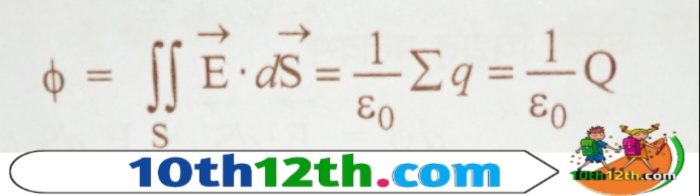
जहां Q, उस पृष्ठ के अंदर स्थित समस्त आवेशों का योग है तथा ε₀, वायु या निर्वात की विद्युतशीलता है। आवेश चाहे बिंदु आवेश हो या सतत वितरित आवेश हो, प्रत्येक स्थिति में यह नियम लागू होता है। यदि पृष्ठ के अंदर आवेश शून्य हैं, पृष्ठ के बाहर स्थित है तो।

इस प्रकार, किसी बंद पृष्ठ से सम्बध्द विद्युत फ्लक्स के मान पर उस पृष्ठ के बाहर स्थित आवेशों का कोई प्रभाव नहीं पड़ता है और न ही इसका मान इस बात पर निर्भर करता है कि पृष्ठ के अंदर आवेश कहां स्थित है।

गौस प्रमेय उपपत्ति

यह निम्न प्रकार से होते हैं -

परिस्थिति (1) जबकि आवेश पृष्ठ के अंदर है

जैसा कि आप चित्र में देख रहे हैं की त्रिज्या r के एक गोले के केंद्र O पर एक बिंदु धनावेश Q स्थित है।

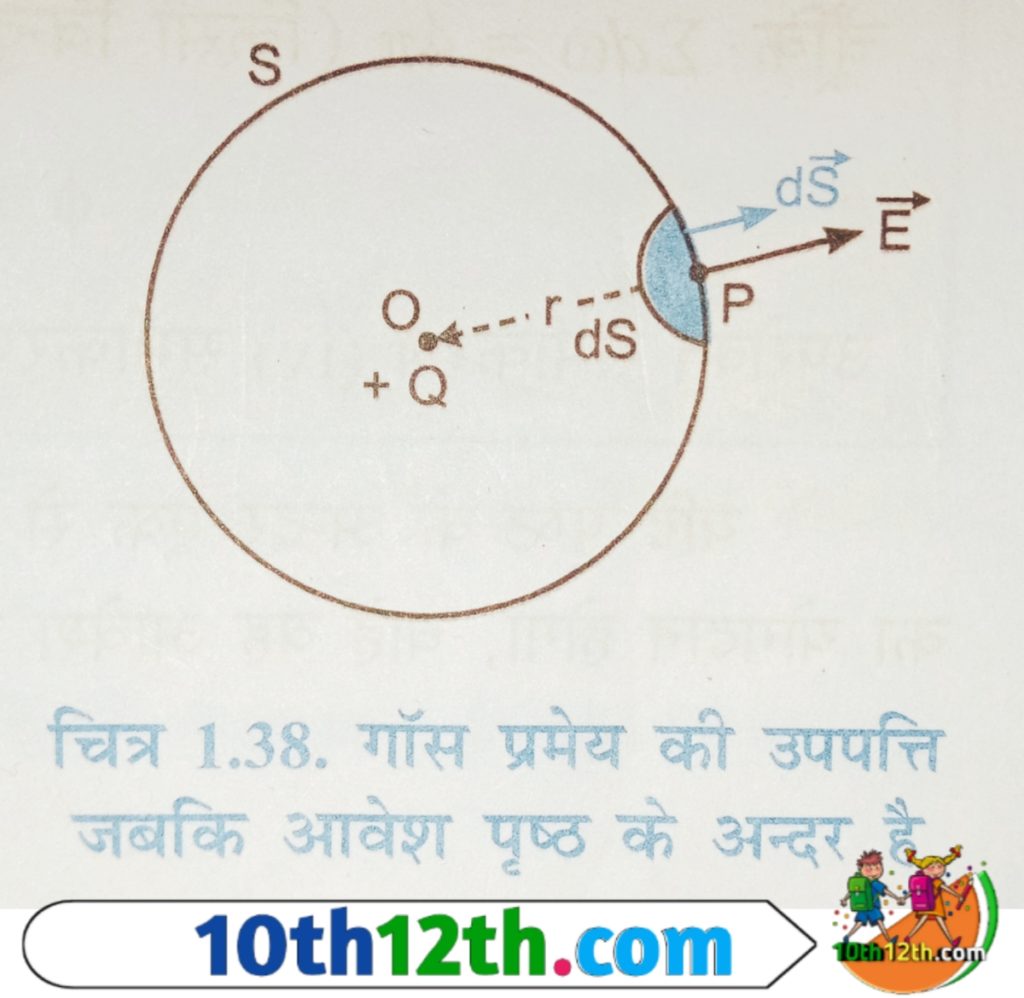
गोले के पृष्ठ पर एक बिंदु P है जिसके चारों ओर एक छोटा-सा क्षेत्रफल अवयव ds है। क्षेत्रफल सदिश ds की दिशा पृष्ठ की लंबवत है। कूलाम नियम अनुसार गोले के पृष्ठ पर स्थित बिंदु P पर आवेश Q के कारण विद्युत क्षेत्र।

चूंकि क्षेत्रफल सदिश ds तथा विद्युत क्षेत्र E एक ही दिशा में है, अतः क्षेत्रफल अवयव ds से सम्बध्द विद्युत फ्लक्स।

अब गोले के संपूर्ण पृष्ठ S से होकर गुजरने वाले विद्युत फ्लक्स का मान ज्ञात करने के लिए पृष्ठ S को ds के समान अनेक छोटे-छोटे भागों में विभाजित करके उनमें से गुजरने वाले फ्लक्स को जोड़ दिया जाता है। अतः संपूर्ण पृष्ठ S से गुजरने वाला फ्लक्स।

परिस्थिति (2) जबकि पृष्ठ के अंदर कोई आवेश नहीं है

जैसा कि आप चित्र में देख रहे हैं कि बाहर स्थित किसी आवेश के कारण उत्पन्न एकसमान विद्युत क्षेत्र E में एक बेलन रखा है जिसकी ज्यामितीय अक्ष, विद्युत क्षेत्र की दिशा के अनुदिश है।

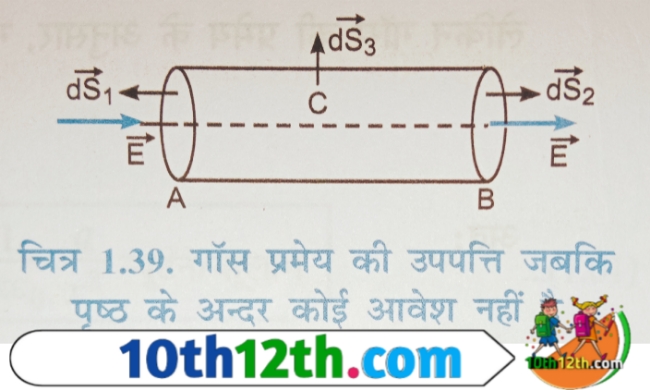
चित्र से स्पष्ट है कि बेलन के पृष्ठ A के क्षेत्रफल सदिश ds₁ की दिशा, विद्युत क्षेत्र E की दिशा के विपरीत है, अतः इससे सम्बध्द विद्युत फ्लक्स
∅ₐ = ₋ E ds₁
बेलन के पृष्ठ B के क्षेत्रफल सदिश ds₂ की दिशा, विद्युत क्षेत्र E की दिशा के अनुदिश है, अतः इससे सम्बध्द विद्युत फ्लक्स
∅b = E ds₂

बेलन के वक्र पृष्ठ C के क्षेत्रफल सदिश ds₃ की दिशा, विद्युत क्षेत्र E के लंबवत है, अतः बेलन के वक्र पृष्ठ सम्बध्द विद्युत फ्लक्स
∅c = 0 अतः संपूर्ण बेलन से सम्बध्द कुल विद्युत फ्लक्स ∅ = ∅a + ∅b + ∅c = – E ds₁ + E ds₂ + 0 =0

क्योंकि बेलन के प्रत्येक वृताकार परिच्छेद का क्षेत्रफल बराबर होता है अर्थात् ds₁ = ds₂ इस प्रकार बेलन, जिसके अंदर कोई आदेश नहीं है, से सम्बध्द कुल विद्युत फ्लक्स शून्य हैं। यही गौस की प्रमेय है। ध्यान रहे कि गौस की प्रमेय किसी भी आकृति के बंद पृष्ठ के लिए सत्य है। यहां केवल सुविधा के लिए गोलाकार या बेलनाकार बंद पृष्ठ कल्पना की गयी है। बंद पृष्ठ को गाउसियन पृष्ठ (gaussian surface) कहते हैं।

गौस की प्रमेय के अनुप्रयोग

गौस की प्रमेय का उपयोग किसी दिए गए आवेश वितरण के कारण किसी बिंदु पर विद्युत क्षेत्र तीव्रता ज्ञात करने के लिए किया जा सकता है। इसके लिए सर्वप्रथम हम ऐसे पृष्ठ की कल्पना करते हैं जो दिये गये आवेश वितरण के परितः सममित हो तथा जिस बिंदु पर हमें विद्युत क्षेत्र की तीव्रता की गणना करनी है, वह बिंदु उस पृष्ठ पर स्थित हो। इस पृष्ठ को गाउसियन पृष्ठ (gaussian surface) कहते हैं। तत्पश्चात गौस की प्रमेय के अनुसार इस पृष्ठ से होकर गुजरने वाले विद्युत फ्लक्स की गणना करते हैं।

महत्वपूर्ण तथ्य

1. गौस की प्रमेय इस तथ्य पर आधारित है कि बिंदु आवेश के कारण विद्युत क्षेत्र की तीव्रता दूरी के वर्ग के व्युत्क्रानुपाती होती है।
2. गौस की प्रमेय का उपयोग मुख्यतः सममित आवेश वितरण के कारण विद्युत क्षेत्र की तीव्रता ज्ञात करने के लिए किया जाता है।
3. गाउसियन पृष्ठ इस प्रकार लेना चाहिए कि इस पर कोई आवेश नहीं हो। गौस की प्रमेय अनुसार बिंदु धनावेश q से चारों ओर निकलने वाली कुल विद्युत क्षेत्र रेखाओं की संख्या q/ε₀ होती है।
4. गौस की प्रमेय गुरुत्वीय क्षेत्र के लिए भी लागू होती है।