रैखिक बहुपद की परिभाषा

चर के गुणांक तथा ऋणेतर घातांक के जोड़, घटाव या गुणन की क्रिया वाले बीजगणितीय पद को बहुपद कहते है। किसी भिन्न वाले घातांक जैसे कि √x , क्योंकि इसे x12 x 1 2 तरह लिखा जाता है। लेकिन एक बहुपद में चर, अचर या घात हो सकते हैं।

रैखिक बहुपद क्या है?

एक रैखिक बहुपद इस रूप का प्रथम अंश बहुपद है- एक बहुपद को रैखिक कहा जाता है यदि इसमें एक चर होता है, इसकी डिग्री (घातीय शक्ति) 1 के बराबर होती है।

इसे p(x) =ax+b की तरह से व्यक्त किया जा सकता है

a₁, a₀ ∈C के लिए। ग्राफिक रूप से, जैसा कि नाम से ही स्पष्ट है, एक सीधी रेखा जिसमें a₁ ढाल (ढलान) को परिभाषित करता है और a₀ कुछ अवरोधन (संदर्भ के फ्रेम के आधार पर) को परिभाषित करता है।

P(x)=a1x+a0 

रैखिक बहुपद सिद्धांत और अनुप्रयोग दोनों में गणित की संपूर्णता में व्याप्त हैं। शायद इस तरह के बहुपदों के बारे में मेरी पसंदीदा चीजों में से एक यह है कि डिग्री n∈N के किसी भी बहुपद को n रैखिक बहुपदों के उत्पाद के रूप में कैसे दर्शाया जा सकता है। प्रतीकात्मक रूप से, इसे इस प्रकार व्यक्त किया जाता है। 

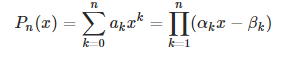
जहाँ αk, βk, ak∈C और βk, Pn का k वाँ मूल है।

यह प्रभावी रूप से रैखिक बहुपदों को बहुपद बीजगणित के दायरे में "बिल्डिंग ब्लॉक्स" की तरह बनाता है, इसी तरह से कि कैसे प्राइम नंबर बाकी प्राकृतिक संख्याओं के लिए ब्लॉक बना रहे हैं।

एक रैखिक बहुपद घात एक का बहुपद होता है, अर्थात, चर का उच्चतम घातांक एक होता है, जिसे इस रूप के समीकरण द्वारा परिभाषित किया जाता है: p(x): ax + b, a≠0। नीचे रैखिक बहुपदों के कुछ उदाहरण दिए गए हैं: p(x): 2x + 3. q(y): y + 2।

रैखिक बहुपद की परिभाषा (Linear Polynomial)

मान लिया कि 4x + 2 एक बहुपद है। इस बहुपद के चर x का घात एक (1) है। अत: इस बहुपद(polynomial) को एक घात वाला बहुपद(polynomial) या रैखिक बहुपद एक घातीय बहुपद कहा जाता हैं। द्विघात शब्द क्वाड्रेट (quadrate) शब्द से बना है, जिसका अर्थ है 'वर्ग'। अत: घात 1 के बहुपद को एक घात वाला बहुपद या रैखिक बहुपद (Linear polynomial) भी कहते हैं।

उदाहरण के लिए: 2x - 3, 3x + 5, y+ 2 , x -2, 3: +4, +1, इत्यादि सभी रैखिक बहुपद हैं। जबकि 2x + 5 - x, x + 1, ओर भी कई प्रकार के बहुपद, रैखिक बहुपद नहीं होते हैं।

द्विघात बहुपद किसे कहते हैं (quadratic polynomial )

जिस बहुपद में चर की अधिकतम घात 2 है और वह शून्य के बराबर नहीं है, वह द्विघात बहुपद है। इसका अर्थ है दूसरी डिग्री का बहुपद। कुछ उदाहरण हैं:

3x2+5x−7 , 17x2–37x+23 , और πx2−2–√x+24 । 

सामान्य रूप है: ax2+bx+c , जहां a,b और c संख्याएं हैं और x एक चर है। ध्यान दें कि उपसर्ग "क्वाड" का अर्थ 4 है, लेकिन ऐसा इसलिए है क्योंकि हल करने की मूल विधि, यानी x के मान ज्ञात करें जो द्विघात बहुपद को शून्य बनाते हैं, "वर्ग को पूरा करना" है, अर्थात द्विघात बहुपद को वर्ग के रूप में लिखना है एक रैखिक बहुपद। वर्गों में 4 भुजाएँ होती हैं, जिससे द्विघात के "चतुर्भुज" की व्याख्या होती है।

द्विघात फलन, द्विघात बहुपद, घात 2 का बहुपद, या केवल द्विघात, एक या अधिक चरों वाला एक बहुपद फलन है जिसमें उच्चतम-डिग्री पद दूसरी डिग्री का होता है। उदाहरण के लिए, तीन चर x, y, और z में एक द्विघात फ़ंक्शन में विशेष रूप से x^2,y^2,z^2, xy, xz, yz, x, y, z, और एक स्थिरांक शामिल हैं:

f(x,y,z)=ax2+by2+cz2+dxy+exz+fyz+gx+hy+iz+j,